2  Methods

2.1 Pre-Processing

2.1.1 Case Selection

Prior to pre-processing, samples were split into a training, a confirmation, and a validation set.

• Training
  • CS1: OOU, OOUE, VOA, MAYO, MTL
  • CS2: OOU, OOUE, VOA, MAYO, OVAR3, OVAR11, JAPAN, MTL, POOL-CTRL
  • CS3: OOU, OOUE, VOA, POOL-1, POOL-2, POOL-3
• Confirmation:
  • CS3: TNCO
• Validation:
  • CS3: DOVE4

2.1.2 Quality Control

Before normalization, we calculated several quality control measures and excluded samples that failed to achieve sample quality in one or more of these measures.

• Linearity of positive control genes: If the R-squared from a linear model of positive controls and their concentrations is less than 0.95 or missing, then the sample is flagged.
• Imaging quality: The sample is flagged if the field of view percentage is less than 75%.
• Positive Control flag: We consider the two smallest positive controls at concentrations 0.5 and 1. If these two controls are less than the lower limit of detection (defined as two standard deviations below the mean of the negative control expression), or if the mean negative control expression is 0, the sample is flagged.
• The signal-to-noise ratio or percent of genes detected: These two measures are defined as the ratio of the average housekeeping gene expression over the upper limit of detection, defined as two standard deviations above the mean of the negative control expression (or 0 if this limit is less than 0.001), and the proportion of endogenous genes with expression greater than the upper limit of detection. These measures are flagged if they are below a pre-specified threshold, which is determined visually by considering their bivariate distribution in a scatterplot. In this case, we used 100 for the SNR threshold and 50% for the threshold for genes detected. Note: these thresholds were determined by examining the relationship in Section 3.3.2.

2.1.3 Housekeeping Genes Normalization

The full training set (n=1257) comprised of data from three CodeSets (CS) 1, 2, and 3. Data normalization removes technical variation from high-throughput platforms to improve the validity of comparative analyses.

Each CodeSet was first normalized to housekeeping genes: ACTB, RPL19, POLR1B, SDHA, and PGK1. Housekeeping genes encode proteins responsible for basic cell function and have consistent expression in all cells. All expression values were log2 transformed. Normalization to housekeeping genes corrects the viable RNA from each sample. This is achieved by subtracting the average log (base 2)-transformed expression of the housekeeping genes from the log (base 2)-transformed expression of each gene:

\[ log_2(\text{endogenous gene expression}) - \text{average(}log_2(\text{housekeeping gene expresssion})) = \text{relative expression} \tag{2.1}\]

2.1.4 Between CodeSet and Site Normalization

To normalize between CodeSets, we randomly selected five specimens, one from each histotype, among specimens repeated in all three CodeSets. This formed the reference set (Random 1). We selected only one sample from each histotype to use as few samples as possible for normalization and retain the rest for analysis.

A reference-based approach (Talhouk et al. (2016)) was used to normalize CS1 to CS3 and CS2 to CS3 across their common genes:

\[ \text{X-Norm}_{\text{CS1}} = X_{\text{CS1}} + {\bar{R}_{\text{CS3}}} - {\bar{R}_{\text{CS1}}} \\ \text{X-Norm}_{\text{CS2}} = X_{\text{CS2}} + {\bar{R}_{\text{CS3}}} - {\bar{R}_{\text{CS2}}} \tag{2.2}\]

Samples in CS3 were processed at three different locations; we also had to normalize for “site” in this CodeSet. Finally, the CS3 expression samples were included in the training set without further normalization:

\[ \text{X-Norm}_{\text{CS3-USC}} = X_{\text{CS3-USC}} + {\bar{R}_{\text{CS3-VAN}}} - {\bar{R}_{\text{CS3-USC}}} \\ \text{X-Norm}_{\text{CS3-AOC}} = X_{\text{CS3-AOC}} + {\bar{R}_{\text{CS3-VAN}}} - {\bar{R}_{\text{CS3-AOC}}} \tag{2.3}\]

Finally, the CS3 expression samples were included in the training set without further normalization. The initial training set is assembled by combining all four of the previously mentioned normalized datasets along with the two CS3 expression subsets not used in normalization:

\[ \begin{aligned} \text{Training Set} &= \text{X-Norm}_{\text{CS1}} + \text{X-Norm}_{\text{CS2}} + \text{X-Norm}_{\text{CS3-USC}} + \text{X-Norm}_{\text{CS3-AOC}} + \text{X-Norm}_{\text{CS3}} + \text{X-Norm}_{\text{CS3-VAN}} \\ &= \text{X-Norm}_{\text{CS1}} + \text{X-Norm}_{\text{CS2}} + \text{X-Norm}_{\text{CS3}} \end{aligned} \tag{2.4}\]

Figure 2.1: Venn diagram of common and unique gene targets covered by each CodeSet

2.1.5 Final Processing

We map ovarian histotypes to all remaining samples and keep the major histotypes for building the predictive model: high-grade serous carcinoma (HGSC), clear cell ovarian carcinoma (CCOC), endometrioid ovarian carcinoma (ENOC), low-grade serous carcinoma (LGSC), mucinous carcinoma (MUC).

Duplicate cases (two samples with the same ottaID) were removed before generating the final training set to use for fitting the classification models. All CS3 cases were preferred over CS1 and CS2, and CS3-Vancouver cases were preferred over CS3-AOC and CS3-USC when selecting duplicates.

The final training set used only genes that were common across all three CodeSets.

Figure 2.2: Cohorts Selection

2.2 Classifiers

We use 4 classification algorithms in the supervised learning framework for the Training Set. The pipeline was run using SLURM batch jobs submitted to a partition on a CentOS 7 server. All resampling techniques, pre-processing, model specification, hyperparameter tuning, and evaluation metrics were implemented using the tidymodels suite of packages. The classifiers we used are:

• Random Forest (rf)
• Support Vector Machine (svm)
• XGBoost (xgb)
• Regularized Multinomial Regression (mr)

2.2.1 Resampling of Training Set

We used a nested cross-validation design to assess each classifier while also performing hyperparameter tuning. An outer 5-fold CV stratified by histotype was used together with an inner 5-fold CV with 2 repeats stratified by histotype. This design was chosen such that the test sets of the inner resamples would still have a reasonable number of samples belonging to the smallest minority class.

The outer resampling method cannot be the bootstrap, because the inner training and inner test sets will likely contain the same samples as a result of sampling with replacement in the outer training set. This phenomenon might result in inflated performance as some observations are used both to train and evaluate the hyperparameter tuning in the inner loop.

2.2.2 Hyperparameter Tuning

The following specifications for each classifier were used for tuning hyperparameters:

• rf and xgb: The number of trees were fixed at 500. Other hyperparameters were tuned across 10 randomly selected points in a latin hypercube design.
• svm: Both the cost and sigma hyperparameters were tuned across 10 randomly selected points in a latin hypercube design. We tuned the cost parameter in the range [1, 8]. The range for tuning the sigma parameter was obtained from the 10% and 90% quantiles of the estimation using the kernlab::sigest() function.
• mr: We generated 10 randomly selected points in a latin hypercube design for the penalty (lambda) parameter. Then, we generated 10 evenly spaced points in [0, 1] for the mixture (alpha) parameter in the regularized multinomial regression model. These two sets of 10 points were crossed to generate a tuning grid of 100 points.

The hyperparameter combination that resulted in the highest average F1-score across the inner training sets was selected for each classifier to use as the model for assessing prediction performance in the outer training loop.

2.2.3 Subsampling

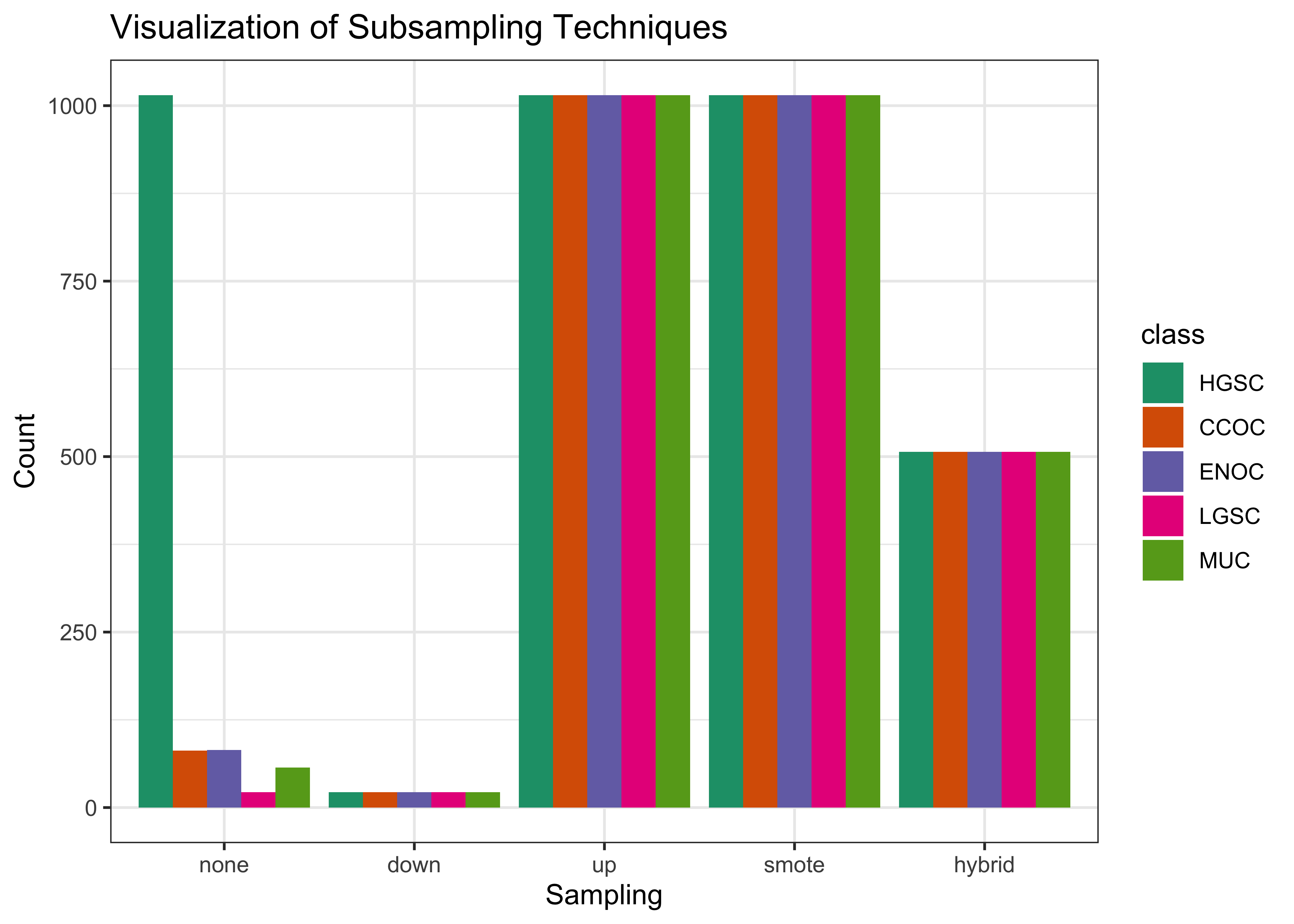
Here are the specifications of the subsampling methods used to handle class imbalance:

• None: No subsampling is performed
• Down-sampling: All levels except the minority class are sampled down to the same frequency as the minority class
• Up-sampling: All levels except the majority class are sampled up to the same frequency as the majority class
• SMOTE: All levels except the majority class have synthetic data generated until they have the same frequency as the majority class
• Hybrid: All levels except the majority class have synthetic data generated up to 50% of the frequency of the majority class, then the majority class is sampled down to the same frequency as the rest.

The figure below helps visualize how the distribution of classes changes when we apply subsampling techniques to handle class imbalance:

Figure 2.3: Visualization of Subsampling Techniques

2.2.4 Workflows

The 4 algorithms and 5 subsampling methods are crossed to create 20 different classification workflows. For example, the hybrid_xgb workflow is a classifier that first pre-processes a training set by applying a hybrid subsampling method, and then proceeds to use the XGBoost algorithm to classify ovarian histotypes.

2.3 Two-Step Algorithm

The HGSC histotype comprises of approximately 80% of cases among ovarian carcinoma patients, while the remaining 20% of cases are relatively, evenly distributed among ENOC, CCOC, LGSC, and MUC histotypes. We can implement a two-step algorithm as such:

• Step 1: use binary classification for HGSC vs. non-HGSC
• Step 2: use multinomial classification for the remaining non-HGSC classes

Let

\[ \begin{aligned} & X_k = \text{Training data with k classes} \\ & C_k = \text{Class with highest}\;F_1\;\text{score from training}\;X_k \\ & W_k = \text{Workflow associated with}\;C_k \end{aligned} \tag{2.5}\]

Figure 2.4 shows how the two-step algorithm works:

Figure 2.4: Two-Step Algorithm

2.3.1 Aggregating Predictions

The aggregation for two-step predictions is quite straightforward:

1. Predict HGSC vs. non-HGSC
2. Among all non-HGSC cases, predict CCOC vs. LGSC vs. MUC vs. ENOC

Figure 2.5: Aggregating Predictions for Two-Step Algorithm

2.4 Sequential Algorithm

Instead of training on k classes simultaneously using multinomial classifiers, we can use a sequential algorithm that performs k-1 one-vs-all binary classifications iteratively to obtain a final prediction of all cases. At each step in the sequence, we classify one class vs. all other classes, where the classes that make up the “other” class are those not equal to the current “one” class and excluding all “one” classes from previous steps. For example, if the “one” class in step 1 was HGSC, the “other” classes would include CCOC, ENOC, LGSC, and MUC. If the “one” class in step 2 was CCOC, the “other” classes include ENOC, LGSC, and MUC.

The order of classes and workflows to use at each step in the sequential algorithm must be determined using a retraining procedure. After removing the data associated with a particular class, we retrain using the remaining data using multinomial classifiers as described before. The class and workflow to use for the next step in the sequence is selected based on the best per-class evaluation metric value (e.g. F1-score).

Figure 2.6 illustrates how the sequential algorithm works for K=5, using ovarian histotypes as an example for the classes.

Figure 2.6: Sequential Algorithm

The subsampling method used in the first step of the sequential algorithm is used in all subsequent steps in order to maintain data pre-processing consistency. As a result, we are only comparing classification algorithms within one subsampling method across the entire sequential algorithm.

2.4.1 Aggregating Predictions

We have to aggregate the one-vs-all predictions from each of the sequential algorithm workflows in order to obtain a final class prediction on a holdout test set. Each sequential workflow has to be assessed on every sample to ensure that cases classified into the “all” class from a previous step of the sequence are eventually assigned a predicted class. For example, say that based on certain class-specific metrics we determined that the order of classes in the sequential algorithm was to predict HGSC vs. non-HGSC, CCOC vs. non-CCOC, LGSC vs. non-LGSC, and then MUC vs. ENOC. Figure 2.7 illustrates how the final predictions are assigned:

Figure 2.7: Aggregating Predictions for Sequential Algorithm

2.5 Performance Evaluation

2.5.1 Class Metrics

We use the accuracy, sensitivity, specificity, F1-score, kappa, balanced accuracy, and geometric mean, as class metrics to measure both training and test performance between different workflows. Multiclass extensions of these metrics can be calculated except for F1-score, where we use macro-averaging to obtain an overall metric. Class-specific metrics are calculated by recoding classes into one-vs-all categories for each class.

2.5.1.1 Accuracy

The accuracy is defined as the proportion of correct predictions out of all cases:

\[ \text{accuracy} = \frac{TP}{TP + FP + FN + TN} \tag{2.6}\]

2.5.1.2 Sensitivity

Sensitivity is the proportional of correctly predicted positive cases, out of all cases that were truly positive

\[ \text{sensitivity} = \frac{TP}{TP + FN} \tag{2.7}\]

2.5.1.3 Specificity

Specificity is the proportional of correctly predicted negative cases, out of all cases that were truly negative.

\[ \text{specificity} = \frac{TN}{TN + FP} \tag{2.8}\]

2.5.1.4 F1-Score

The F-measure can be thought of as a harmonic mean between precision and recall:

\[ F_{meas} = \frac{(1 + \beta^2) \times precision \times recall}{(\beta^2 \times precision) + recall} \tag{2.9}\]

The \(\beta\) value can be adjusted to place more weight upon precision or recall. The most common value is \(\beta\) is 1, which is also commonly known as the F1-score. A multiclass extension doesn’t exist for the F1-score, so we use macro-averaging to calculate this metric when there are more than two classes. For example, with \(k\) classes, the macro-averaged F1-score is equal to:

\[ {F_1}_{macro} = \frac{1}{k} \sum_{i=1}^{k}{F_1}_{i} \tag{2.10}\]

where each \({F_1}_{i}\) is the F1-score computed frrom recoding classes into \(k=i\) vs. \(k \neq i\).

In situations where there is not at least one predicted case for each of the classes (e.g. for a poor classifier), \({F_1}_{i}\) is undefined because the per-class precision of class \(i\) is undefined. Those \({F_1}_{i}\) terms are removed from the \({F_1}_{macro}\) equation and the resulting value may be inflated. Interpreting the F1-score in such a case would be misleading.

2.5.1.5 Balanced Accuracy

Balanced accuracy is the arithmetic mean of sensitivity and specificity.

\[ \text{Balanced Accuracy} = \frac{\text{Sensitivity} + \text{Specificity}}{2} \tag{2.11}\]

2.5.1.6 Kappa

Kappa is the defined as:

\[ \text{kappa} = \frac{p_0 - p_e}{1 - p_e} \tag{2.12}\]

where \(p_0\) is the observed agreement among raters and \(p_e\) is the hypothetical probability of agreement due to random chance.

2.5.2 AUC

The area under the receiver operating curve (AUC) is calculated by adding up the area under the curve formed by plotting sensitivity vs. 1 - specificity. The Hand-till method is used as a multiclass extension for the AUC.

We did not use AUC to measure class-specific training set performance because combining predicted probabilities in a one-vs-all fashion might be potentially misleading. The sum of probabilities that add up to the “other” class is not equivalent to the predicted probability of the “other” class when using a multiclass classifier.

Instead, we only reported ROC curves and their associated AUCs for test set performance among the highest ranked algorithms.

2.6 Rank Aggregation

To select the best algorithm, we implemented a two-stage rank aggregation procedure using the Genetic Algorithm. First, we ranked all workflows based on per-class F1-scores, balanced accuracy, and kappa to see which workflows performed well in predicting all five histotypes. Then, we took the ranks from these three performance metrics and performed a second run of rank aggregation. The top 5 workflows were determined from the final rank aggregation result.

2.7 Gene Optimization

We want to discover an optimal set of genes for the classifiers while including specific genes from other studies such as PrOTYPE and SPOT. A total of 72 genes are used in the classifier training set.

There are 16 genes in the classifier set that overlap with the PrOTYPE classifier: COL11A1, CD74, CD2, TIMP3, LUM, CYTIP, COL3A1, THBS2, TCF7L1, HMGA2, FN1, POSTN, COL1A2, COL5A2, PDZK1IP1, FBN1.

There are also 13 genes in the classifier set that overlap with the SPOT signature: HIF1A, CXCL10, DUSP4, SOX17, MITF, CDKN3, BRCA2, CEACAM5, ANXA4, SERPINE1, TCF7L1, CRABP2, DNAJC9.

We obtain a total of 28 genes from the union of PrOTYPE and SPOT genes that we want to include in the final classifier, regardless of model performance. We then incrementally add genes one at a time from the remaining 44 candidate genes based on a variable importance rank to the set of 28 base genes and recalculate performance metrics. The number of genes at which the performance peaks or starts to plateau may indicate an optimal gene set model for us to compare with the full set model.

Here is the breakdown of genes used and whether they belong to the PrOTYPE and/or SPOT sets:

Table 2.1: Gene Distribution

Genes	PrOTYPE	SPOT
TCF7L1	✔	✔
COL11A1	✔
CD74	✔
CD2	✔
TIMP3	✔
LUM	✔
CYTIP	✔
COL3A1	✔
THBS2	✔
HMGA2	✔
FN1	✔
POSTN	✔
COL1A2	✔
COL5A2	✔
PDZK1IP1	✔
FBN1	✔
HIF1A		✔
CXCL10		✔
DUSP4		✔
SOX17		✔
MITF		✔
CDKN3		✔
BRCA2		✔
CEACAM5		✔
ANXA4		✔
SERPINE1		✔
CRABP2		✔
DNAJC9		✔
C10orf116
GAD1
TPX2
KGFLP2
EGFL6
KLK7
PBX1
LIN28B
TFF3
MUC5B
FUT3
STC1
BCL2
PAX8
GCNT3
GPR64
ADCYAP1R1
IGKC
BRCA1
IGJ
TFF1
MET
CYP2C18
CYP4B1
SLC3A1
EPAS1
HNF1B
IL6
ATP5G3
DKK4
SENP8
CAPN2
C1orf173
CPNE8
IGFBP1
WT1
TP53
SEMA6A
SERPINA5
ZBED1
TSPAN8
SCGB1D2
LGALS4
MAP1LC3A

2.7.1 Variable Importance

Variable importance is calculated using either a model-based approach if it is available, or a permutation-based VI score otherwise. The variable importance scores are averaged across the outer training folds, and then ranked from highest to lowest.

For the sequential and two-step classifiers, we calculate an overall VI rank by taking the cumulative union of genes at each variable importance rank across all sequences, until all genes have been included.

The variable importance measures are:

• Random Forest: impurity measure (Gini index)

• XGBoost: gain (fractional contribution of each feature to the model based on the total gain of the corresponding features’s splits)

• SVM: permutation based p-values

• Multinomial regression: absolute value of estimated coefficients at cross-validated lambda value

Talhouk, Aline, Stefan Kommoss, Robertson Mackenzie, Martin Cheung, Samuel Leung, Derek S. Chiu, Steve E. Kalloger, et al. 2016. “Single-Patient Molecular Testing with NanoString nCounter Data Using a Reference-Based Strategy for Batch Effect Correction.” Edited by Benjamin Haibe-Kains. PLOS ONE 11 (4): e0153844. https://doi.org/10.1371/journal.pone.0153844.